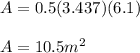Question

For the following question, find the area of the triangle. give the answer to the nearest tenth. The drawing may not be to scale

Answer 1

option A

10.5 m²

Explanation:

Given in the question,

base of triangle = 6.1 m

one side of triangle = 4.7m

one angle = 47°

To find the area of this triangle we will use the following formula

Area = 1/2 (height)(base)

Step1

Find height by using trigonometry identity

sinФ = opp/hyp

sin(47) = height/4.7

height = 3.44m

Step2

Plug values in the formula of area

(0.5)(6.1)(3.43)

10.48m²

≈10.5m²

Answer 2

Option A

10.5 m²

Explanation:

The area of a triangle is half the product of its base by its height.

`A = 0.5bh`

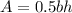
Where b is the base and h is the height.

In this triangle b = 6.1 m.

The height of this triangle is a line perpendicular to its base that goes to the vertex opposite the base.

We do not know this length. But this line h divides the triangle into two rectangular triangles.

So for these two triangles the angle that is opposite to the height h is: 47 °

Therefore we know that senx is defined as:

`senx =(opposite side)/(hypotenuse)`

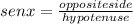
Where:

Opposite side = h

hypotenuse = 4.7 m

x = 47

`Sin(47) = (h)/(4.7)\\\\h = (sin47)(4.7)\\\\h = 3.437`

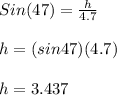
Finally, the area is:

`A = 0.5(3.437)(6.1)\\\\A = 10.5m^2`