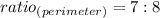Question

The figures are similar. Give the ratio of the perimeters and the ratio of the areas of the first figure to the second.

Answer 1

Answer: first option.

Explanation:

The ratio of the area of the triangles can be calculated as following:

`ratio_((area))=((l_1)/(l_2))^2`

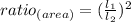
Where
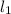`l_1` is the lenght of the given side of the smaller triangle and
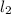`l_2` is the lenght of the given side of the larger triangle.

Therefore:

`ratio_((area))=((28)/(32))^2=(49)/(64)`

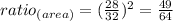
It can be written as following:

`ratio_((area))=49:64`

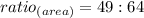
The ratio of the perimeter is:

`ratio_((perimeter))=(l_1)/(l_2)`

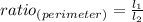
Where
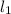`l_1` is the lenght of the given side of the smaller triangle and
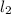`l_2` is the lenght of the given side of the larger triangle.

Therefore:

`ratio_((perimeter))=(28)/(32)=(7)/(8)`

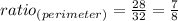
It can be written as following:

`ratio_((perimeter))=7:8`