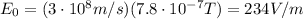Question

The helium-neon lasers most commonly used in student physics laboratories have average power outputs of 0.250 mW.

(a) If such a laser beam is projected onto a circular spot 2.10 mm in diameter, what is its intensity?
(b) Find the peak magnetic field strength.
(c) Find the peak electric field strength.

Answer 1

(a)
`72.3 W/m^2`

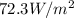
First of all, we need to find the area of the circular spot, which is given by:

`A=\pi r^2`

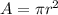
where r is the radius of the spot, which is half the diameter, therefore

`r=(d)/(2)=(2.10 mm)/(2)=1.05 mm=1.05\cdot 10^(-3) m`

So, the area of the spot is

`A=\pi (1.05\cdot 10^(-3)m)^2=3.46\cdot 10^(-6) m^2`

We know that the power output of the laser is

`P=0.250 mW=2.5\cdot 10^(-4) W`

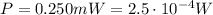
So the intensity of the laser beam is

`I=(P)/(A)=(2.5\cdot 10^(-4) W)/(3.46\cdot 10^(-6) m^2)=72.3 W/m^2`

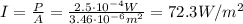
(b)
`7.8\cdot 10^(-7)T`

The average intensity of the laser is related to the peak magnetic field strength by

`I=(cB_0^2)/(2\mu_0)`

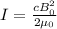
where

c is the speed of light

`B_0` is the peak magnetic field strength

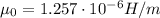`\mu_0=1.257\cdot 10^(-6) H/m` is the vacuum magnetic permeability

Solving the formula for
`B_0`, we find

`B_0 = \sqrt{(2I\mu_0)/(c)}=\sqrt{(2(72.3 W/m^2)(1.257\cdot 10^(-6) H/m))/(3\cdot 10^8 m/s)}=7.8\cdot 10^(-7)T`

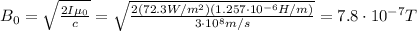
(c) 234 V/m

The relationship between magnetic field and electric field in an electromagnetic wave is

`E_0=cB_0`

where

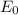`E_0` is the peak electric field strength

c is the speed of light

`B_0` is the peak magnetic field strength

Substituting numbers into the formula, we find

`E_0=(3\cdot 10^8 m/s)(7.8\cdot 10^(-7) T)=234 V/m`