Question

Find the area of the trapezoid. leave your answer in simplest radical form.

Answer 1

170 ft²

Explanation:

We can divide this figure into two parts.

We have the rectangle part and the triangle,

Area of the triangle = 1/2 bh

base = 22 - 12 = 10 ft

height = 10×tan 45°

= 10 × 1 = 10 ft

∴ Area = 1/2 × 10 × 10

= 50 ft²

Area of the rectangle = length × width

length = 12 ft

width = 10 ft

Area = 12 × 10

= 120 ft²

Total area of the trapezoid = 120 + 50

= 170 ft²

Answer 2

Area = 170 ft^2

Explanation:

Area of Trapezoid is given by the formula
`A=(1)/(2)(b_1+b_2)h`

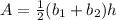
Where

b1 and b2 are the two bases (parallel sides)

h is the height

In our diagram, the two bases are 12 and 22, but the height (let it be h) isn't given. To find the height (the dotted line), we use the right triangle which has an angle given as 45°.

Since the height is the "opposite" side to angle and we know the base of the triangle (22-12=10), which is the "adjacent" side, we can use the ratio of tan. Note, tan 45° = 1.

`Tan(45)=(h)/(10)\\h=Tan(45)*10\\h=1*10\\h=10`

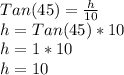
Now we can plug the information into the formula and solve for area. So:

Area =
`A=(1)/(2)(b_1+b_2)h\\A=(1)/(2)(12+22)(10)\\A=(1)/(2)(34)(10)\\A=170`

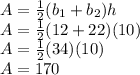
Thus Area = 170 ft^2