Question

Find the quotient -5+12i/ 3-3 square root 3i using trigonometric forms

Answer 1

2.433

Explanation:

using

a+bi=r(cosP+isinP)

Let

-5 =
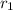`r_(1)`cosФ

12 =
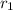`r_(1)`sinФ

Taking square both on both sides

(-5)² + (12)² =
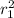`r_(1)^2`cos²Ф +
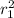`r_(1)^2`sin²Ф

we know that

sin²Ф + cos²Ф = 1

25 + 144 =
`r_(1)^2`(1)

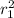`r_(1)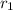` = √(144 + 25)

= 13

Similarly,

Let

-3 =
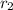`r_(2)`cosФ

-3√3 =
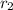`r_(2)`sinФ

taking square both on both sides

(-3)² + (-3√3)² =
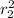`r_(2)^2`cos²Ф +
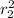`r_(2)^2`sin²Ф

we know that

sin²Ф + cos²Ф = 1

9 + 27 =
`r_(2)^2`(2)

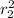`r_(2)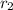` = √(9 + 27)

= 6

Also

`(r_(1)sin\alpha )/(r_(1)cos\alpha ) = (12)/(-5)`

`\alpha = r_(1)tan^(-1) ((12)/(-5) )`

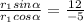
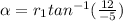
And

`(r_(2)sin\alpha )/(r_(2)cos\alpha ) = (-3√(3) )/(3)\\`

`\alpha = r_(2)tan^(-1) (-3√(3) )/(3)`

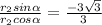
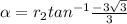
So

`(-5+12i)/(3-3√(3i) )` =
`(13tan^(-1)(-12)/(5))/(6tan^(-1)(-√(3)))`

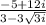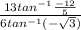
= 2.433