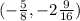Question

Find the equation of the axis of symmetry and the coordinates of the vertex of the graph of y=4x^2+5x-1

c) x=-5/8; vertex (-5/8, -5 11/16)
D) x=-5/8; vertex (-5/8, -2 9/16)

​

Answer 1

Answer:

Axis of symmetry:
`x=-(5)/(8)`

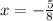
Vertex:
`(-(5)/(8),-2(9)/(16))`

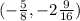
Explanation:

The given quadratic equation is


`y=4x^2+5x-1`

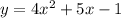
By comparing to the general quadratic function;
`y=ax^2+bx+c`

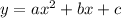
We have a=4,b=5,c=-1

The equation of the axis of symmetry is given by the formula;


`x=-(b)/(2a)`

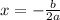
We got this formula by completing the square on the general quadratic function.

We substitute a=4 and b=5 to obtain;


`x=-(5)/(2(4))`


`x=-(5)/(8)`
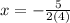
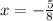
is the axis of symmetry.

To find the y-value of the vertex, we put
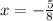
`x=-(5)/(8)` into the function to obtain;


`y=4(-(5)/(8))^2+5(-(5)/(8))-1`


`y=4(-(5)/(8))^2+5(-(5)/(8))-1`


`y=-(41)/(16)`

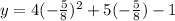
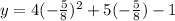
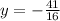
The vertex of the given function is
`(-(5)/(8),-2(9)/(16))`