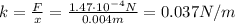Answer:
0.037 N/m
Step-by-step explanation:
The web acts as a spring, so it obeys Hook's law:
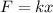 (1)
(1)
where
F is the force exerted on the web
k is the spring constant
x is the stretching/compression of the web
In this problem, we have:
- The mass of the fly is
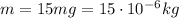
- The force exerted on the web is the weight of the fly, so:

- The stretching of the web is
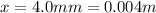
So if we solve eq.(1) for k, we find the spring constant: