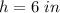1 Answer

Dalvenjia · Answer 1 · 2020-10-19T17:27:39+0000

Answer:

The radius of the cup is
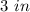$3\ in$ and

the height of the cup is
$6\ in$

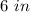
Explanation:

we know that

The volume of the cylinder is equal to

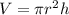
$V=\pi r^(2)h$

Let

x-----> the height and the diameter of the cylinder

we have

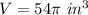
$V=54\pi\ in^(3)$

$h=x\ in$

$D=x\ in$

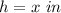
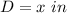
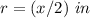
$r=(x/2)\ in$

substitute the values

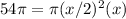
$54\pi=\pi (x/2)^(2)(x)$

simplify

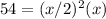
54=(x/2)^(2)(x)

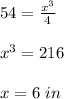
$54=(x^(3))/(4) \\ \\x^(3)=216\\ \\x=6\ in$

therefore

The radius of the cup is

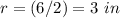
$r=(6/2)=3\ in$

The height of the cup is

$h=6\ in$

Please log in or register to add a comment.