Question

How do the lengths of line segments define the golden ratio?

Answer 1

`(a+b)/(a)=(a)/(b)`

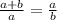
Explanation:

The golden ratio is a special number favored by the Greeks. Its ratio roughly equals 1.618. The ratio is formed by taking a line segment and dividing it into two parts labeled a and b. The golden ratio is formed when this proportion is true
`(a+b)/(a)=(a)/(b)`.

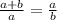When you add a and b then divide by a, it will be the same as a divided by b. This will hold true only for specific lengths of a and b. This means you must divide the line segment in such a way that a and b meet this requirement.

Example:

If the line segment is 50 cm long. Split the segment into parts a and b where a = 30.9 and b = 19.1. Substitute the values into the proportion
`(a+b)/(a)=(a)/(b)`.

`(30.9+19.1)/(30.9)=(30.9)/(19.1)`

`(50)/(30.9)=(30.9)/(19.1)`

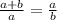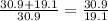
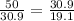
1.618 = 1.618

This is the golden ratio.