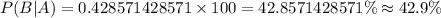Answer: 42.9%
Explanation:
From the given table , the number of part-time jobs =6+8 = 14
Total jobs = 6+8+9+2=25
Let A be the event of selecting a part time job , then
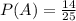
Let B be the event of selecting a job where experience is needed.
The number of part time job openings where experience is needed =
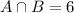
Then,
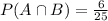
Now, the probability that experience is needed for a randomly selected job opening, given that it is for part-time work is given by :-
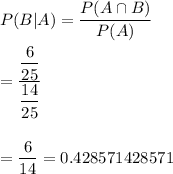
In percent,