Question

Consider the hydrogen atom. How does the energy difference between adjacent orbit radii change as the principal quantum number increases?

Answer 1

the energy difference between adjacent levels decreases as the quantum number increases

Step-by-step explanation:

The energy levels of the hydrogen atom are given by the following formula:

`E=-E_0 (1)/(n^2)`

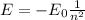
where

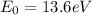`E_0 = 13.6 eV` is a constant

n is the level number

We can write therefore the energy difference between adjacent levels as

`\Delta E=-13.6 eV ((1)/(n^2)-(1)/((n+1)^2))`

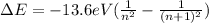
We see that this difference decreases as the level number (n) increases. For example, the difference between the levels n=1 and n=2 is

`\Delta E=-13.6 eV((1)/(1^2)-(1)/(2^2))=-13.6 eV(1-(1)/(4))=-13.6 eV((3)/(4))=-10.2 eV`

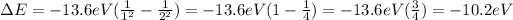
While the difference between the levels n=2 and n=3 is

`\Delta E=-13.6 eV((1)/(2^2)-(1)/(3^2))=-13.6 eV((1)/(4)-(1)/(9))=-13.6 eV((5)/(36))=-1.9 eV`

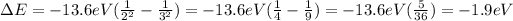
And so on.

So, the energy difference between adjacent levels decreases as the quantum number increases.