Question

For 3–5, suppose the heights of a group of children are normally distributed with a mean of 38.36 inches and a standard deviation 2.14 inches.

3. What percent of the children are taller than 42.64 inches tall?

4. What percent of the children are shorter than 36.22 inches tall?

5. What percent of the children are between 34.08 and 42.64 inches tall?

Answer 1

3) 2.5%

4) 16%

5) 95%

Explanation:

Mean = u = 38.36 inches

Standard Deviation = s = 2.14 inches

Formula for z-score =
`(x-u)/(s)`

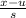
Question 3)

We have to find what percent of children are taller than 42.64 inches. We can do this by converting 42.64 to z-score.

Here, x = 42.64

Using the formula mentioned above, we get:

`z=(42.64-38.36)/(2.14)=2`

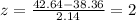
According to the Empirical Rule, 95% of the values lie within 2 standard deviations of the mean. This means 5% of the value lie outside 2 standard deviations and half of these i.e. 2.5% will be above 2 standard deviations.

Therefore, we can say that 2.5% of the children are taller than 42.64 inches.

Question 4)

Here x = 36.22

Using the formula mentioned above, we get:

`z=(36.22-38.36)/(2.14)=-1`

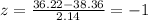
According to empirical rule, 68% of the values lie within 1 standard deviation of the mean. This means, remaining 32% are outside the 1 standard deviation and from these half of the values i.e. 16% are below 1 standard deviation.

Therefore, we can say that 16% of the children are shorter than 36.22 inches.

Question 5)

We have to find what percent of children are between 34.08 and 42.64

34.08 converted to z-score = -2

42.64 converted to z-score = 2

According to the empirical rule, 95% of the data values are within 2 standard deviations of the mean.

So, we can conclude that 95% of the children are between 34.08 and 42.64 inches tall.