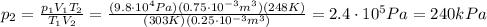Question

A sample of gas with a volume of 750 mL exerts a pressure of 98 kPa at 30 °C.What pressure will the sample exert when it is compressed to 250 mL and cooled to -25 °C?

Answer 1

240 kPa

Step-by-step explanation:

The ideal gas law states:

`pV=nRT`

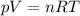
where

p is the gas pressure

V is the gas volume

n is the number of moles

R is the gas constant

T is the absolute temperature of the gas

For a fixed amount of gas, n and R are constant, so we can rewrite the equation as

`(pV)/(T)=const.`

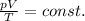
For the gas in the problem, which undergoes a transformation, this can be rewritten as

`(p_1V_1)/(T_1)=(p_2V_2)/(T_2)`

where we have:

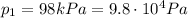`p_1 = 98 kPa=9.8\cdot 10^4 Pa` is the initial pressure

`V_1 = 750 mL=0.75 L=0.75\cdot 10^(-3) m^3` is the initial volume

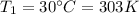`T_1 =30^(\circ)C =303 K` is the initial temperature

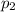`p_2` is the final pressure

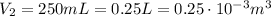`V_2=250 mL=0.25 L=0.25\cdot 10^(-3) m^3` is the final volume

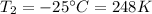`T_2=-25^(\circ)C=248 K` is the final temperature

Solving the formula for p2, we find the final pressure of the gas:

`p_2 = (p_1 V_1 T_2)/(T_1 V_2)=((9.8\cdot 10^4 Pa)(0.75\cdot 10^(-3)m^3)(248 K))/((303 K)(0.25\cdot 10^(-3) m^3))=2.4\cdot 10^5 Pa = 240 kPa`