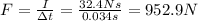(a) 96 m/s
The impulse theorem states that the impulse exerted on the ball is equal to the change in momentum of the ball:
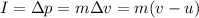
where
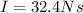 is the impulse exerted on the ball
is the impulse exerted on the ball
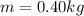 is the mass of the ball
is the mass of the ball
 is the final speed of the ball
is the final speed of the ball
 is the initial speed of the ball
is the initial speed of the ball
Solving the equation for v, we find
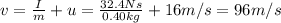
(b) 952.9 N
The impulse is also equal to the product between the average force and the contact time:
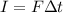
where here we have
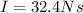 is the impulse
is the impulse
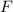 is the average force
is the average force
 is the contact time
is the contact time
Solving the equation for F, we find the force: