Question

If a factory continuously dumps pollutants into a river at the rate of the quotient of the square root of t and 45 tons per day, then the amount dumped after 5 days is

0.166
0.331
1.656
3.333

Answer 1

Hello!

The answer is:

The first option, the amount dumped after 5 days is 0.166 tons.

Why?

To solve the problem, we need to integrate the given expression and evaluate using the given time.

So, integrating we have:

`\int\limits^5_0 {(√(t) )/(45) } \, dt=\int\limits^5_0 {(1)/(45) (t)^{(1)/(2) } } \, dt\\\\\int\limits^5_0 {(1)/(45) (t)^{(1)/(2) } } \ dt=(1)/(45)\int\limits^5_0 {t^{(1)/(2) } } } \ dt\\\\(1)/(45)\int\limits^5_0 {t^{(1)/(2) } } } \ dt=((1)/(45)*\frac{t^{(1)/(2)+1} }{(1)/(2) +1})/t(5)-t(0)\\\\((1)/(45)*\frac{t^{(1)/(2)+1} }{(1)/(2) +1})/t(5)-t(0)=((1)/(45)*\frac{t^{(3)/(2)} }{(3)/(2)})/t(5)-t(0)`

`((1)/(45)*\frac{t^{(3)/(2)} }{(3)/(2)})/t(5)-t(0)=((1)/(45)*(2)/(3)*t^{(3)/(2) })/t(5)-t(0)\\\\((1)/(45)*(2)/(3)*t^{(3)/(2) })/t(5)-t(0)=((2)/(135)*t^{(3)/(2)})/t(5)-t(0)\\\\((2)/(135)*t^{(3)/(2)})/t(5)-t(0)=((2)/(135)*5^{(3)/(2)})-((2)/(135)*0^{(3)/(2)})\\\\((2)/(135)*5^{(3)/(2)})-((2)/(135)*0^{(3)/(2)})=(2)/(135)*11.18-0=0.1656=0.166`

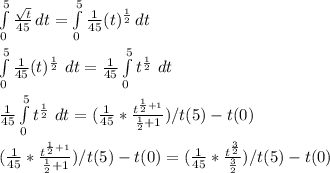
Hence, we have that the amount dumped after 5 days is 0.166 tons.

Have a nice day!