Answer:
Center: (0,0)
Radius:
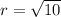
Explanation:
The given circle has equation
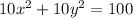
In order to complete the square, we must make sure the coefficient of the quadratic terms are unity.
We divide through by 10 to obtain;
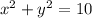
The coefficient of the linear terms of both variables are zero.
Therefore the equation can be rewritten as;
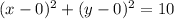
Comparing to

We have (h,k)=(0,0) to the center of the circle and
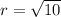 to be the radius of the circle.
to be the radius of the circle.