The median of a set is defined as the middle element of the sorted set.
So, the only way to add two elements without changing the median is to add an element before it, and one element after it.
Think about it: if you are the middle element in a queue, and we add something before you and something after you, you're still in the middle:
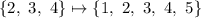
In both cases, the middle element is 3.
If, instead, we add two elements before 3,
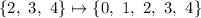
the median has changed, and similarly if we add two elements after 3
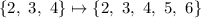
the median has changed again.
So, if we sort our set, we have
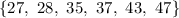
And the middle elements are 35 and 37. The only option that adds something bigger than then and something smaller than them is option a.