Answer:
∠ ECF = 90°
∠AKB = 77.5°
∠ACF = 75°
Explanation:
The given figure is a circle E.
Line CF is tangent at point C.
(1) To find measures of angle ECF
Since line FC is tangent at point C and radius ECis always perpendicular to the tengent.
So ∠ ECF = 90°
(2) Measure of angle AKB
By theorem of angle formed by two interesting chords.
∠ AKB =
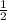 (arc AB + arc CD)
(arc AB + arc CD)
=
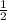 (50 + 105) =
(50 + 105) =
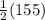
∠AKB = 77.5°
(3) Measure of angle ACF
Since tangent chord angle =
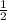 (intercepted arc)
(intercepted arc)
m (∠ACF) =
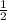 (m arc AB + m arc BC)
(m arc AB + m arc BC)
=
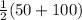
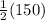
∠ACF = 75°