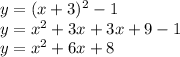Question

I need help with this please

Answer 1

`y = x^2 + 6x + 8`

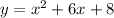
Explanation:

The equation can be written using information from the graph. The vertex of the parabola is (-3,-1). Use the vertex form
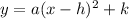`y = a(x-h)^2 + k` by substituting h = -3 and k = -1. The equation becomes
`y = a(x--3)^2 + -1`. It simplifies to
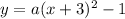`y = a(x+3)^2 - 1`. To find a, substitute the point (x,y) on the graph into the equation and solve for a. Substitute x = -2 and y = 0.

`0 = a(-2+3)^2 - 1`

`0 = a(1)^2 - 1`

`0 = a - 1`

`1 = a`

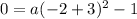
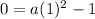
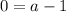
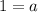
So the equation is
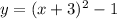`y = (x+ 3)^2 - 1`. Convert to standard form by distributing the parenthesis and combining like terms.

`y = (x+ 3)^2 - 1\\y = x^2 + 3x + 3x + 9 - 1\\y = x^2 + 6x + 8`