Question

You do a certain amount of work on an object initially at rest, and all the work goes into increasing the object’s speed. If you do work W, suppose the object’s final speed is v. What will be the object’s final speed if you do twice as much work? 1. 2 v 2. v/√ 2 3. √ 2 v 4. Still v 5. 4 v

Answer 1

`√(2)v`

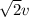
Step-by-step explanation:

The work done on the object at rest is all converted into kinetic energy, so we can write

`W=(1)/(2)mv^2`

Or, re-arranging for v,

`v=\sqrt{(2W)/(m)}`

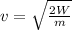
where

v is the final speed of the object

W is the work done

m is the object's mass

If the work done on the object is doubled, we have W' = 2W. Substituting into the previous formula, we can find the new final speed of the object:

`v'=\sqrt{(2W')/(m)}=\sqrt{(2(2W))/(m)}=√(2)\sqrt{(2W)/(m)}=√(2)v`

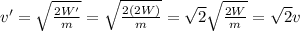
So, the new speed of the object is
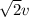`√(2)v`.