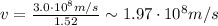Answer:
It decreases
Step-by-step explanation:
The speed of light in a vacuum is
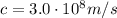
When it travels into a medium, however, light slows down. the speed of light in a medium is given by the equation
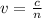
where
v is the speed of light in the medium
c is the speed of light in a vacuum
n is the refractive index of the medium
We see that the larger the refractive index of the medium, the lower the speed of light in that medium. For air, water and glass we have:
Air:
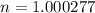
Water:
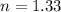
Glass:
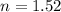
So we can calculate the speed of light in the three mediums:
Air:
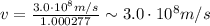
Water:
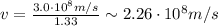
Glass: