Answer:
1/9 of that just outside the smaller sphere
Step-by-step explanation:
The electric field strength produced by a charged sphere outside the sphere itself is equal to that produced by a single point charge:

where
k is the Coulomb's constant
Q is the charge on the sphere
r is the distance from the centre of the sphere
Calling R the radius of the first sphere, the electric field just outide the surface of the first sphere is
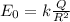
The second sphere has a radius which is 3 times that of the smaller sphere:

So, the electric field just outside the second sphere is
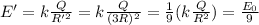
So, the correct answer is 1/9.