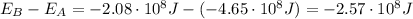1 Answer

Rix · Answer 1 · 2020-11-19T00:33:42+0000

(a) 0.448

The gravitational potential energy of a satellite in orbit is given by:

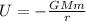
U=-(GMm)/(r)

where

G is the gravitational constant

M is the Earth's mass

m is the satellite's mass

r is the distance of the satellite from the Earth's centre, which is sum of the Earth's radius (R) and the altitude of the satellite (h):

r = R + h

We can therefore write the ratio between the potentially energy of satellite B to that of satellite A as

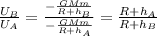
(U_B)/(U_A)=(-(GMm)/(R+h_B))/(-(GMm)/(R+h_A))=(R+h_A)/(R+h_B)

and so, substituting:

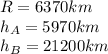
$R=6370 km\\h_A = 5970 km\\h_B = 21200 km$

We find

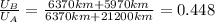
(U_B)/(U_A)=(6370 km+5970 km)/(6370 km+21200 km)=0.448

(b) 0.448

The kinetic energy of a satellite in orbit around the Earth is given by

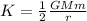
K=(1)/(2)(GMm)/(r)

So, the ratio between the two kinetic energies is

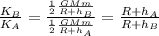
(K_B)/(K_A)=((1)/(2)(GMm)/(R+h_B))/((1)/(2)(GMm)/(R+h_A))=(R+h_A)/(R+h_B)

Which is exactly identical to the ratio of the potential energies. Therefore, this ratio is also equal to 0.448.

(c) B

The total energy of a satellite is given by the sum of the potential energy and the kinetic energy:

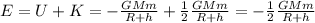
E=U+K=-(GMm)/(R+h)+(1)/(2)(GMm)/(R+h)=-(1)/(2)(GMm)/(R+h)

For satellite A, we have

$E_A=-(1)/(2)(GMm)/(R+h_A)=-(1)/(2)((6.67\cdot 10^(-11))(5.98\cdot 10^(24)kg)(28.8 kg))/(6.37\cdot 10^6 m+5.97\cdot 10^6 m)=-4.65\cdot 10^8 J$

For satellite B, we have

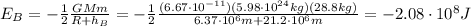
$E_B=-(1)/(2)(GMm)/(R+h_B)=-(1)/(2)((6.67\cdot 10^(-11))(5.98\cdot 10^(24)kg)(28.8 kg))/(6.37\cdot 10^6 m+21.2\cdot 10^6 m)=-2.08\cdot 10^8 J$

So, satellite B has the greater total energy (since the energy is negative).

(d)
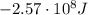
$-2.57\cdot 10^8 J$

The difference between the energy of the two satellites is:

$E_B-E_A=-2.08\cdot 10^8 J-(-4.65\cdot 10^8 J)=-2.57\cdot 10^8 J$

Please log in or register to add a comment.