Question

What is the perimeter of a triangle with the vertices located at (1,3), (2,6), and (0,4), rounded to the nearest hundredth?

A. 7.40 units
B. 9.07 units
C. 8.49 units
D. 7.07 units

Answer 1

The correct answer option is A. 7.40 units.

Explanation:

We are given the following coordinates of the vertices of a triangle and we are to find its perimeter:

(1,3), (2,6), and (0,4)

Finding the lengths of all three sides:

AB =
`\sqrt { ( 1 - 2 ) ^ 2 + ( 3 - 6 ) ^ 2 } = √(10) =3.16`

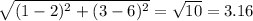
BC =
`\sqrt { ( 2 - 0 ) ^ 2 + ( 6 - 4 ) ^ 2 } = √(8) =2.83`

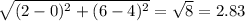
CA =
`\sqrt { ( 0 - 1 ) ^ 2 + ( 4 - 3 ) ^ 2 } = √(2) =1.41`

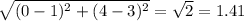
Perimeter of the triangle =
`3.16+2.83+1.41` = 7.40 units

Answer 2

Answer: OPTION A

Explanation:

You can plot the points given in the problem, as you can see in the figure attached.

Apply the formula for calculate the distance between two points, which is:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

Distance AB:

`d_(AB)=√((2-1)^2+(6-3)^2)=3.162units`

Distance AC:

`d_(AC)=√((0-1)^2+(4-3)^2)=1.414units`

Distance BC:

`d_(BC)=√((2-0)^2+(6-4)^2)=2.828units`

The perimeter is:

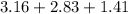`P=3.162units+1.414units+2.828units\\P=7.40units`