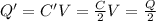Question

The charge on the square plates of a parallel-plate capacitor is Q. The potential across the plates is maintained with constant voltage by a battery as they are pulled apart to twice their original separation, which is small compared to the dimensions of the plates. The amount of charge on the plates is now equal toA)4QB)2QC)QD)Q/2E)Q/4

Answer 1

D) Q/2

Step-by-step explanation:

The relationship between charge Q, capacitance C and voltage drop V across a capacitor is

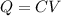`Q=CV` (1)

In the first part of the problem, we have that the charge stored on the capacitor is Q, when the voltage supplied is V. The capacitance of the parallel-plate capacitor is given by

`C=(\epsilon_0 A)/(d)`

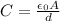
where
`\epsilon_0` is the vacuum permittivity, A is the area of the plates, d is the separation between the plates.

Later, the voltage of the battery is kept constant, V, while the separation between the plates of the capacitor is doubled:
`d'=2d`. The capacitance becomes

`C'=(\epsilon_0 A)/(d')=(\epsilon_0 A)/(2d)=(C)/(2)`

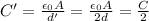
And therefore, the new charge stored on the capacitor will be

`Q'=C'V=(C)/(2)V=(Q)/(2)`