Answer:
Connect them in parallel
Step-by-step explanation:
The energy stored by two capacitors connected to the same voltage source is given by
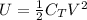
where
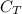 is the total capacitance of the two capacitors
is the total capacitance of the two capacitors
V is the voltage of the source
In order to maximize the energy stored U, we need to maximize
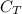 . We have:
. We have:
- In parallel, the total capacitance is given by the sum of the individual capacitances:

- In series, the total capacitance is given by:
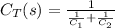
Comparing the two equations, we notice that
 , so the parallel configuration is the one that maximizes the energy stored.
, so the parallel configuration is the one that maximizes the energy stored.