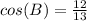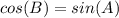Question

I need help with this question.

For the right triangle shown match the equivalent expressions.

Answer 1

The solution in the attached figure

`sin(A)=(12)/(13)`

`sin(B)=(5)/(13)`

`cos(A)=(5)/(13)`

`cos(B)=(12)/(13)`

`sin(A)=cos(B)`

`sin(B)=cos(A)`

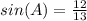
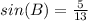
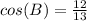
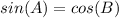
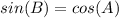
Explanation:

we know that

In the right triangle ABC

sin(A)=cos(B) and cos(A)=sin(B)

because

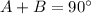`A+B=90\°` -------> by complementary angles

step 1

Find sin(A)

The function sine of angle A is equal to divide the opposite side angle A by the hypotenuse

`sin(A)=(BC)/(AB)`

substitute the values

`sin(A)=(12)/(13)`

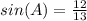
step 2

Find sin(B)

The function sine of angle B is equal to divide the opposite side angle B by the hypotenuse

`sin(B)=(AC)/(AB)`

substitute the values

`sin(B)=(5)/(13)`

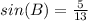
step 3

Find cos(A)

The function cosine of angle A is equal to divide the adjacent side angle A by the hypotenuse

`cos(A)=(AC)/(AB)`

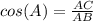
substitute the values

`cos(A)=(5)/(13)`

`cos(A)=sin(B)`

step 4

Find cos(B)

The function cosine of angle B is equal to divide the adjacent side angle B by the hypotenuse

`cos(B)=(BC)/(AB)`

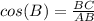
substitute the values

`cos(B)=(12)/(13)`

`cos(B)=sin(A)`