Question

I need help plz. Binary math

Answer 1

Answer: A) 63

========================================================

Step-by-step explanation:

Whenever you have a series of nothing but '1's like this, the base 10 equivalent is always going to be 1 less than a power of 2.

The number will be of the form
`2^n-1` where n is a nonnegative integer.

If you're familiar with the list of powers of 2, then you'll likely realize that 64 is a power of 2 since
`2^6 = 64`. One less than this is
`2^6-1 = 64-1 = 63`

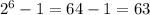
This leads to choice A as the answer.

The other answer choices are not one less than a power of 2, so we can cross those off the list.

------------------------------

Further explanation:

Each slot in the binary number given represents a power of 2. We multiply those '1's by a power of 2 and add them up like so

1*(2^5) + 1*(2^4) + 1*(2^3) + 1*(2^2) + 1*(2^1) + 1*(2^0)

1*32 + 1*16 + 1*8 + 1*4 + 1*2 + 1*1

32 + 16 + 8 + 4 + 2 + 1

63

Summing the first n powers of 2 leads to the result
`2^(n)-1`

So, summing the first 6 powers of 2 leads to
`2^n-1 = 2^6-1 = 63`