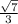Answer:
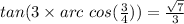
Explanation:
The given expression is
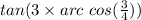
Where
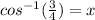 , which means that,
, which means that,
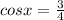
If we analyse this trigonometric reason in a right triangle, we would find the hypothenuses is 4 and the adjacent leg is 3. Then, using pythagorean theorem, we find the other leg
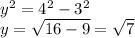
Which means the opposite leg of our right triangle is the square root of seven.
Finally, using such right triangle, we find the tangent reason, which is the quotient between the opposite leg and the adjacent leg
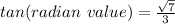
Therefore, the answer is