Question

Hotels’ use of ecolabels. Refer to the Journal of Vacation Marketing (January 2016) study of travelers’ familiarity with ecolabels used by hotels, Exercise 2.64 (p. 80). Recall that adult travelers were shown a list of 6 different ecolabels, and asked, “Suppose the response is measured on a continuous scale from 10 (not familiar at all) to 50 (very familiar).” The mean and standard deviation for the Energy Star ecolabel are 44 and 1.5, respectively. Assume the distribution of the responses is approximately normally distributed a. Find the probability that a response to Energy Star ex- ceeds 43 between 42 and 45 think it is likely that t b. Find the probability that a respo nse to Energy Star falls c. If you observe a response of 35 to an ecolabel, do vou he ecolabel was Energy Star? Explain.

Answer 1

a) 0.7486; b) 0.6518; c) No

Explanation:

We use z scores to answer these questions. The formula for a z score is

`z=(X-\mu)/(\sigma)`

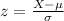
Our mean, μ, is 44; our standard deviation, σ, is 1.5.

For part a,

We want P(X > 43):

z = (43-44)/1.5 = -1/1.5 = -0.67

Using a z table, we see that the area under the curve to the left of this is 0.2514. However, we want the area to the right; this means we subtract from 1:

1 - 0.2514 = 0.7486

For part b,

We want P(42 ≤ X ≤ 45):

z = (42-44)/1.5 = -2/1.5 = -1.3

z = (45-44)/1.5 = 1/1.5 = 0.67

Using a z table, the area under the curve to the left of z = -1.3 is 0.0968. The area under the curve to the left of z = 0.67 is 0.7486.

The area between them is 0.7486 - 0.0968 = 0.6518.

For part c,

A response of 35 has a z score of

z = (35-44)/1.5 = -9/1.5 = -6

This is 6 standard deviations below the mean. This is more than the amount required to make this an outlier, or an unlikely response.