Answer:
a)The temperature of the gas in increased by four times its original value.
Step-by-step explanation:
For a fixed amount of a gas, the ideal gas equation can be written as follows:
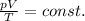
where
p is the gas pressure
V is the gas volume
T is the gas temperature (in Kelvins)
For a gas under transformation, the equation can also be rewritten as

where the labels 1,2 refer to the initial and final conditions of the gas.
In this problem, we have:
- The pressure of the gas is doubled:
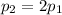
- The volume of the gas is doubled:
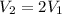
Substituting into the equation, we find what happens to the temperature:
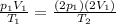
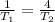

So, the correct choice is
a)The temperature of the gas in increased by four times its original value.