Question

Find the minimum value of the function for the polygonal convex set determined by the given system of inequalities.

3x+2y≥14
-8x+3y≤10
f(x,y)=8x+8y

Answer 1

Option b (4,1)

Explanation:

The region given by the system of inequalities is shown in the graph. We must look within this region for the point that minimizes the objective function
`f(x, y) = 8x + 8y`

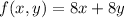
The minimum points are found in the lower vertices of the region.

These vertices are found by equating the equations of the lines::

`3x+2y=14\\-5x +5y=10`

-------------------

`x = 2\\y = 4`

`-8x + 3y = -29\\3x + 2y = 14`

---------------------

`x = 4\\y = 1`

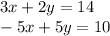
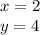
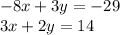
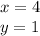
The lower vertices are:

(4, 1) (2, 4)

Now we substitute both points in the objective function to see which of them we get the lowest value of
`f(x, y)`

`f(4, 1) = 8(4) +8(1) = 40\\f(2, 4) = 8(2) + 8(4) = 48`

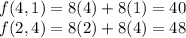
Then the value that minimizes f(x, y) is (4,1).

Option b