Question

A 0.42 kg mass is attached to a light spring with a force constant of 34.9 N/m and set into oscillation on a horizontal frictionless surface. If the spring is stretched 5.0 cm and released from rest, determine the following. (a) maximum speed of the oscillating mass .45578 Correct: Your answer is correct. m/s (b) speed of the oscillating mass when the spring is compressed 1.5 cm .43478 Correct: Your answer is correct. m/s (c) speed of the oscillating mass as it passes the point 1.5 cm from the equilibrium position .43478 Correct: Your answer is correct. m/s (d) value of x at which the speed of the oscillating mass is equal to one-half the maximum value

Answer 1

(a) 0.456 m/s

The maximum speed of the oscillating mass can be found by using the conservation of energy. In fact:

- At the point of maximum displacement, the mechanical energy of the system is just elastic potential energy:

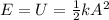`E=U=(1)/(2)kA^2` (1)

where

k = 34.9 N/m is the spring constant

A = 5.0 cm = 0.05 m is the amplitude of the oscillation

- At the point of equilibrium, the displacement is zero, so all the mechanical energy of the system is just kinetic energy:

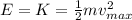`E=K=(1)/(2)mv_(max)^2` (2)

where

m = 0.42 kg is the mass

vmax is the maximum speed, which is maximum when the mass passes the equilibrium position

Since the mechanical energy is conserved, we can write (1) = (2):

`(1)/(2)kA^2=(1)/(2)mv_(max)^2\\v_(max)=\sqrt{(kA^2)/(m)}=\sqrt{((34.9 N/m)(0.05 m)^2)/(0.42 kg)}=0.456 m/s`

(b) 0.437 m/s

When the spring is compressed by x = 1.5 cm = 0.015 m, the equation for the conservation of energy becomes:

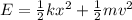`E=(1)/(2)kx^2+(1)/(2)mv^2` (3)

where the total mechanical energy can be calculated at the point where the displacement is maximum (x = A = 0.05 m):

`E=(1)/(2)kA^2=(1)/(2)(34.9 N/m)(0.05 m)^2=0.044 J`

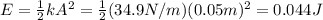
So, solving (3) for v, we find the speed when x=1.5 cm:

`v=\sqrt{(2E-kx^2)/(m)}=\sqrt{(2(0.044 J)-(34.9 N/m)(0.015 m)^2)/(0.42 kg)}=0.437 m/s`

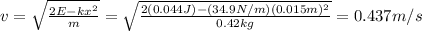
(c) 0.437 m/s

This part of the problem is exactly identical to part b), since the displacement of the mass is still

x = 1.5 cm = 0.015 m

So, the speed when this is the displacement is

`v=\sqrt{(2E-kx^2)/(m)}=\sqrt{(2(0.044 J)-(34.9 N/m)(0.015 m)^2)/(0.42 kg)}=0.437 m/s`

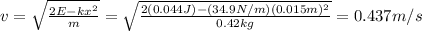
(d) 4.4 cm

In this case, we have that the speed of the mass is 1/2 of the maximum value, so:

`v=(v_(max))/(2)=(0.456 m/s)/(2)=0.228 m/s`

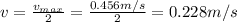
And by using the conservation of energy again, we can find the corresponding value of the displacement x:

`E=(1)/(2)kx^2+(1)/(2)mv^2\\x=\sqrt{(2E-mv^2)/(k)}=\sqrt{(2(0.044 J)-(0.42 kg)(0.228 m/s)^2)/(34.9 N/m)}=0.044 m=4.4 cm`