Question

Mr. Williams is building a sand box for his children. It costs $228 for the sand if he builds a rectangular-sand box with dimensions 9 ft by 6 ft. How much will the sand cost if he decides to increase the size to 1312 ft by 9 ft? A. $513 B. $289 C. $342 D. $380

Answer 1

A. $513

Explanation:

Find the area of the boxes by multiplying the sides.

The first box is 54 ft sq.

The second box is 121.5 ft sq.

So

`\\(54)/(121.5) =(228)/(x)`

cross mult.

27702 = 54x

513 = x

Answer 2

Answer: The correct option is (C) $342.

Step-by-step explanation: Given that Mr. Williams is building a sand box for his children and is costs $228 for the sand if he builds a rectangular-sand box with dimensions 9 ft by 6 ft.

We are to find the cost of the sand if he decides to increase the size to
`13(1)/(2)~\textup{ft by }9~\textup{ft}.`

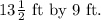
Since the box is empty from inside, so we will be considering the perimeter of the box, not area.

The perimeter of the rectangular-sand box with dimensions 9 ft by 6 ft is

`P_1=2(9+6)=30~\textup{ft},`

and the perimeter of the rectangular-sand box with dimensions
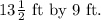`13(1)/(2)~\textup{ft by }9~\textup{ft}.` is

`P_2=2\left(13(1)/(2)*9\right)=2(13.5*9)=45~\textup{ft}.`

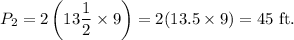
Now, we will be using the UNITARY method.

Cost of sand for building rectangular-sand box with perimeter 30ft = $228.

So, cost of sand for building rectangular-sand box with perimeter 1 ft will be

`\$(228)/(30).`

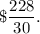
Therefore, the cost of sand for building rectangular-sand box with perimeter 45 ft is given by

`\$(228)/(30)*45=\$342.`

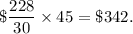
Thus, the required cost of the sand is $342.

Option (C) is CORRECT.