Question

A rectangle has a length that is 2 meters more than the width. The area of the rectangle is 288 square meters. Find the dimensions of the rectangle.

Answer 1

L = 18 and w = 16

Explanation:

The area of a rectangle is found by A = l*w. Since the length here is 2 more than the width or 2 + w and the width is w, substitute these values and A = 288 to solve for w.

`A = l*w\\288 = w(2+w)\\288 = w^2 + 2w`

To solve for w, move 288 to the other side by subtraction. Then factor and solve.

`w^2 + 2w  - 288 = 0 \\(w +18)(w-16) = 0\\`

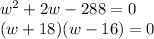
Set each factor equal to 0 and solve.

w - 16 = 0 so w = 16

w + 18 = 0 so w = -18

Since w is a side length and length/distance cannot be negative, then w = 16 is the width of the rectangle.

This means the length is 16 + 2 = 18.