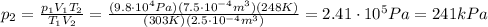Question

A sample of gas with a volume of 750 ml exerts a pressure of 98 kpa at 30◦c. What pressure will the sample exert when it is compressed to 250 ml and cooled to −25◦c?

Answer 1

241 kPA

Step-by-step explanation:

I just did the quest assignment, it was correct

Answer 2

241 kPa

Step-by-step explanation:

The ideal gas law states that:

`pV=nRT`

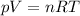
where

p is the gas pressure

V is its volume

n is the number of moles

R is the gas constant

T is the absolute temperature of the gas

We can rewrite the equation as

`(pV)/(T)=nR`

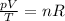
For a fixed amount of gas, n is constant, so we can write

`(pV)/(T)=const.`

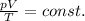
Therefore, for a gas which undergoes a transformation we have

`(p_1 V_1)/(T_1)=(p_2 V_2)/(T_2)`

where the labels 1 and 2 refer to the initial and final conditions of the gas.

For the sample of gas in this problem we have

`p_1 = 98 kPa=9.8\cdot 10^4 Pa\\V_1 = 750 mL=0.75 L=7.5\cdot 10^(-4)m^3\\T_1 = 30^(\circ)C+273=303 K\\p_2 =?\\V_2 = 250 mL=0.25 L=2.5\cdot 10^(-4) m^3\\T_2 = -25^(\circ)C+273=248 K`

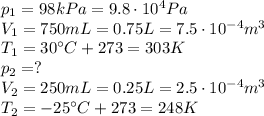
So we can solve the formula for
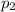`p_2`, the final pressure:

`p_2 = (p_1 V_1 T_2)/(T_1 V_2)=((9.8\cdot 10^4 Pa)(7.5\cdot 10^(-4) m^3)(248 K))/((303 K)(2.5\cdot 10^(-4) m^3))=2.41\cdot 10^5 Pa = 241 kPa`