Question

Solve the following system. x2 + y 2= 25 2x + y = 10 The solution set

Answer 1

Answer: {(5,0), (3,4)}

Explanation:

You can apply the Substitution method:

- Solve for y from the second equation.

- Substitute into the first equation and solve for x.

Then:

`y=10-2x`

`x^2+y^2=25\\x^2+(10-2x)^2=25\\`

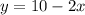
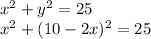
(Remember that:
`(a\±b)^2=a^2\±2ab+b^2`)

`x^2+(10^2-2(10)(2x)+(2x)^2)=25\\x^2+100-40x+4x^2=25\\5x^2-40x+75=0\\x^2-8x+15=0\\(x-5)(x-3)=0\\\\x=5\\x=3`

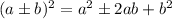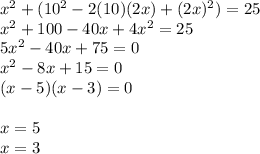
Substitute the values obtained into one of the original equation and solve for y:

`2(5)+y=10\\10+y=10\\y=0\\\\2(3)+y=10\\6+y=10\\y=4`

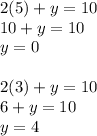
The solution set is: {(5,0), (3,4)}