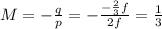Question

An object is placed a distance of twice the focal length away from a diverging lens. What is the magnification of the image?

Answer 1

1/3

Step-by-step explanation:

We can solve the problem by using the lens equation:

`(1)/(f)=(1)/(p)+(1)/(q)`

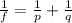
where

f is the focal length

p is the distance of the object from the lens

q is the distance of the image from the lens

Here we have a divering lens, so the focal length must be taken as negative (-f). Moreover, we know that the object is placed at a distance of twice the focal length, so

`p=2f`

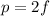
So we can find q from the equation:

`(1)/(q)=(1)/((-f))-(1)/(p)=-(1)/(f)-(1)/(2f)=-(3)/(2f)\\q=-(2)/(3)f`

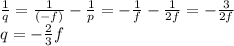
Now we can find the magnification of the image, given by:

`M=-(q)/(p)=-(-(2)/(3)f)/(2f)=(1)/(3)`