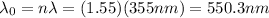1 Answer

Jimwan · Answer 1 · 2020-09-27T08:24:51+0000

A) 1.55

The speed of light in a medium is given by:

v=(c)/(n)

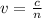
where

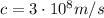$c=3\cdot 10^8 m/s$ is the speed of light in a vacuum

n is the refractive index of the material

In this problem, the speed of light in quartz is

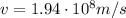
$v=1.94\cdot 10^8 m/s$

So we can re-arrange the previous formula to find n, the index of refraction of quartz:

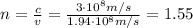
$n=(c)/(v)=(3\cdot 10^8 m/s)/(1.94\cdot 10^8 m/s)=1.55$

B) 550.3 nm

The relationship between the wavelength of the light in air and in quartz is

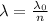
$\lambda=(\lambda_0)/(n)$

where

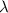$\lambda$ is the wavelenght in quartz

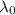$\lambda_0$ is the wavelength in air

n is the refractive index

For the light in this problem, we have

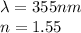
$\lambda=355 nm\\n=1.55$

Therefore, we can re-arrange the equation to find
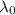$\lambda_0$ , the wavelength in air:

$\lambda_0 = n\lambda=(1.55)(355 nm)=550.3 nm$

Please log in or register to add a comment.