Hello!
The answers are:
B.
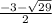
C.
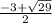
Why?
We can use the quadratic equation to find the two values of x that are roots of the given equation. We must remember that most of the quadratic equations have two roots, however, we could find quadratic equations with just one root or even with no roots, at least in the real numbers.
Quadratic equation:
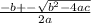
So,
From the given equation we have:
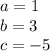
Substituting it into the quadratic equation to find the roots, we have:
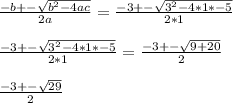
So,
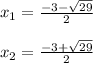
Hence, the correct options are B and C.