Answer:
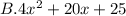
Explanation:
The length of the side:
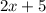
In a square all sides have the same length.
And the area of a square is given by the formula:

so, substituting that the length is
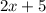
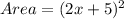
and we solve this squared binomial with the formula:
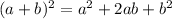
in this case
 and
and
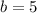
thus, we get:
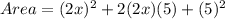
and solving:
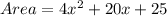
which is option B.