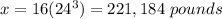Answer:
Part a) The weight of the original statue is
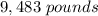
The ratio of the height of the original statue to the height of the small statue is 8.4
The ratio of the weights or volumes is
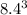
Part b)
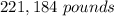
Explanation:
Part a)
we know that
If two figures are similar, then the ratio of its corresponding sides is equal to the scale factor and the ratio of its volumes or weights is equal to the scale factor elevated to the cube
step 1
Find the scale factor
remember that
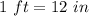
The original statue is 7 ft tall
Convert to inches
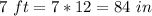
Divide the height of the original statue by the height of the model to find the scale factor
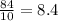
step 2
Find the ratio of its weights
Let
z-----> the scale factor
x-----> the weight of the original statue
y----> the weight of the model
so
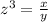
we have
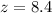

substitute
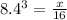
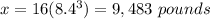
The weight of the original statue is
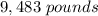
The ratio of the height of the original statue to the height of the small statue is 8.4
The ratio of the weights or volumes is
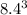
Part b) If the original statue were 20 ft tall, how much would it weight?
step 1
Find the scale factor
remember that
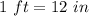
The original statue is 20 ft tall
Convert to inches
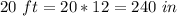
Divide the height of the original statue by the height of the model to find the scale factor
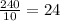
step 2
Find the ratio of its weights
Let
z-----> the scale factor
x-----> the weight of the original statue
y----> the weight of the model
so
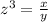
we have
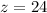

substitute