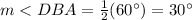Answer:
Part 1)
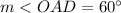
Part 2)
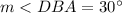
Explanation:
Part 1) Find the measure of angle OAD
we know that
OA=OD=radius of the circle
If line AD≅ line AO
then
The triangle AOD is an equilateral triangle
Remember that
An equilateral triangle has the three equal sides and the three internal angles equal (60 degrees each one)
so
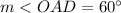
Part 2) Find the measure of angle DBA
we know that
The inscribed angle measures half that of the arc comprising
so
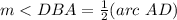
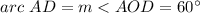 ----> by central angle
----> by central angle
substitute the value