Answer:
We can say that the graph g(x) is obtained by shifting the grapf f(x) by 2 units up.
Explanation:

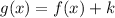
Rule : f(x)→f(x)+k
graph f(x) shifts upward by k units
Since we are given that
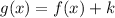
So, this means when graph f(x) shifts upward by k units then g(x) is obtained
We are given that k = 2
So, when graph f(x) shifts upward by 2 units then g(x) is obtained .
Thus we can say that the graph g(x) is obtained by shifting the grapf f(x) by 2 units up.