Question

Can someone please help me with #9? (25 points)

Answer 1

Explanation:

General Solution

Left hand side

tan(30) + 1 / tan(30

tan^2(30) + 1

============

tan 30

but tan^2(30) + 1 = sec^2(30)

sec^2(theta) / tan(30) Let theta = 30o. This will work for any angle between 0 and 90

`(sec^2(theta))/(tan(theta)) = (sec^2(theta))/((sin(theta))/(cos(theta))) = (1)/((cos^2(theta)*sin(theta))/(cos(theta)))`

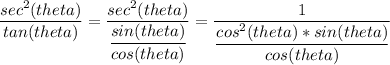
Cancel out cos(theta) and one of cos^2(theta)

leaving your with

`(1)/(sin(theta)*cos(theta))`

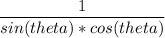
which is exactly what the right hand side is.

This is the way this problem should be done. If you want to show what happens with 30o then

Thirty degree angle

tan(30) = 0.5774

Left hand side

0.5774 + 1/(0.5774) = 2.3093

Right hand side

1/(sin(30)*cos(30))

1/(0.5 * 0.8660)

1/(0.4330

2.3094

Which is about as close as you will get when you round.