Question

An electronics store discovers that it can sell 5 televisions per day by pricing them at $150. When the televisions are on sale for $100 the store sells 10 of them every day. Write a linear equation to compare the price of a television, p, to the number sold, x. Then write a quadratic equation to compare the revenue, m, from selling televisions to the number sold, x.

Answer 1

`p=-10x+200`

`m = -10x^2+200x`

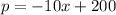
Explanation:

Given : An electronics store discovers that it can sell 5 televisions per day by pricing them at $150. When the televisions are on sale for $100 the store sells 10 of them every day.

To Find: Write a linear equation to compare the price of a television, p, to the number sold, x. Then write a quadratic equation to compare the revenue, m, from selling televisions to the number sold, x.

Solution:

Let p be the price and x be the no. of television sold

We are given that it can sell 5 televisions per day by pricing them at $150. When the televisions are on sale for $100 the store sells 10 of them every day. i.e(5,150) and (10,100)

Now to find the linear equation to compare the price of a television, p, to the number sold, x.

We will use two point slope form

Formula :
`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

`(x_1,y_1)=(5,150)`

`(x_2,y_2)=(10,100)`

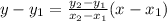
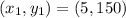
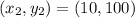
Substitute the values in the formula

`y-150=(100-150)/(10-5)(x-5)`

`y-150=(-50)/(5)(x-5)`

`y-150=-10(x-5)`

`y-150=-10x+50`

`y=-10x+50+150`

`y=-10x+200`

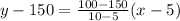
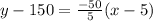
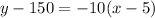
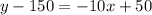
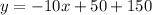
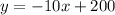
x is the no. of television sold

y is the price

Since p denotes the price

So,
`p=-10x+200`

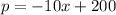
Thus a linear equation to compare the price of a television, p, to the number sold, x is
`p=-10x+200`

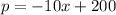
Now
`Revenue = Cost * quantity`

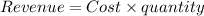
Since price of x telivisons =
`p=-10x+200`

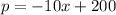
So,
`Revenue = (-10x+200) * x`

`Revenue = -10x^2+200x`

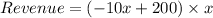
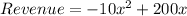
m denotes revenue

So,
`m = -10x^2+200x`

Thus a quadratic equation to compare the revenue, m, from selling televisions to the number sold, x. is
`m = -10x^2+200x`

Hence a linear equation to compare the price of a television, p, to the number sold, x is
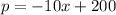`p=-10x+200` and a quadratic equation to compare the revenue, m, from selling televisions to the number sold, x. is
`m = -10x^2+200x`

Answer 2

`p = -10x + 200`

`m = -10x^2 +200x`

Explanation:

We know that at a price of $ 150, 5 televisions are sold and at a price of $ 100, 10 televisions are sold.

We must write a linear equation for this situation.

The equation of the line will have the following form

`p = mx + b`

Where m is the slope of the line and b is the intercept with the p axis

`m=(y_2-y_1)/(x_2-x_1)\\\\m=(100-150)/(10-5)=-10`

`b=p_1-mx_1\\\\b=150-(-10)(5)\\\\b=200`

The equation is:

`p = -10x + 200`

Now we know that the revenue m is the product of the price p for the quantity sold x.

`m = p * x`

`m=(-10x + 200)*x`

`m = -10x^2 +200x`