ANSWER
a. 2 real roots, 2 imaginary roots
Step-by-step explanation
The given equation is
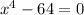
We rewrite as difference of two squares,
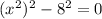
We factor using difference of two squares to get;
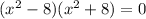
We now use the zero product property to get:

Take the square root of both sides to get;
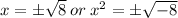
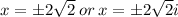

are two real roots.
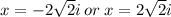
are two imaginary roots.
The correct answer is A.