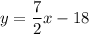Answer:
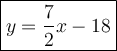
Explanation:
The slope-intercept form of an equation of a line:

Convert the equation of a line 3x + 4x = 2y - 9 to the slope-intercept form:
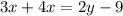
 add 9 to both sides
add 9 to both sides
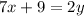 divide both sides by 2
divide both sides by 2
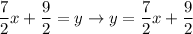
Parallel lines have the same slope. Therefore we have the equation:
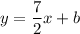
Put the coordinates of the point (4, -4) to the equation:
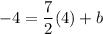
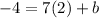
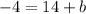 subtract 14 from both sides
subtract 14 from both sides
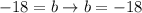
Finally we have the equation: