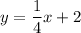The point slope form of the equation of a line that passes through (8,4) and (0,2) is y-4=1/4(×-8) what is the slope intercept form of the equation for this line.

Question

asked Oct 14, 2020 80.9k views

2 Answers

Ryenski · Answer 1 · 2020-10-20T08:34:11+0000

Answer:

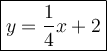
$\large\boxed{y=(1)/(4)x+2}$

Explanation:

The slope-intercept form of the equation of a line:

y=mx+b

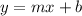
m - slope

b - y-intercept → (0, b)

The point-slope form of the equation of a line:

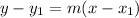
y-y_1=m(x-x_1)

m - slope

(x₁, y₁) - point

We have the equation of a line:

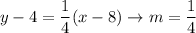
$y-4=(1)/(4)(x-8)\to m=(1)/(4)$

and the point (0, 2) → b = 2.

Substitute:

y=(1)/(4)x+2