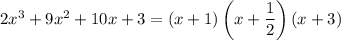Question

Factorise 2x^3+9x^2+10x+3​

Answer 1

In order to factor a polynomial
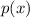`p(x)`, we have to find all its roots
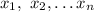`x_1,\ x_2,\ldots x_n` so that we can rewrite the polynomial as

`p(x)=(x-x_1)(x-x_2)\ldots(x-x_n)`

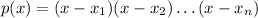
This is exactly the same idea we apply when we factor numbers: we look for all the primes that divide the number, and then we write

`n = p_1^(e_1)\cdot p_2^(e_2)\ldots p_n^(e_n)`

When talking about polynomials, the idea of prime numbers is represented by irreducible polynomials, i.e. polynomials with no roots.

So, we have to find a root of our polynomial. Using the rational root theorem, we can check that
`x=-1` is a solution:

`p(-1)=2(-1)^3+9(-1)^2+10(-1)+3 = -2+9-10+3=0`

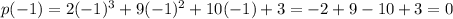
So, our polynomial is divisible by
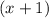`(x+1)`. The long division yields

`(2x^3+9x^2+10x+3​)/(x+1) = 2x^2+7x+3`

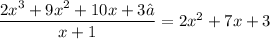
Which is the same as

`2x^3+9x^2+10x+3=(x+1)(2x^2+7x+3)`

We can complete the factorization by breaking the quadratic equation: using the standard quadratic formula we can find the solutions

`2x^2+7x+3=0 \iff x=-(1)/(3)\text{ or }x=-3`

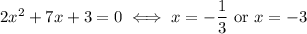
Which implies

`2x^2+7x+3=\left(x+(1)/(2)\right)(x+3)`

And finally

`2x^3+9x^2+10x+3=(x+1)\left(x+(1)/(2)\right)(x+3)`